Logaritma Özellikleri Nelerdir? – Logaritma Fonksiyonu Hakkında Herşey!

Logaritma özellikleri ayrıntılarına geçmeden önce kısa bir tarihine bakacak olursak; Napier tarafından keşfedilen, “Logos” (Latin alfabe oranı) ve “Arithmos” (Latin alfabe sayıları) kelimelerinin birleşimi olarak Logorithmus adını verdiği bir sistem olduğunu görürüz. Bu kelime daha sonraları logaritma olarak Türkçemize tanıtıldı. Matematikte, logaritma, üsleri bulmak için kullanılan işlemdir. Örneğin, 8 sayısı için 2’nin kaç üssüne bakmamız gerekir? Elbette cevap 3’tür (2³ = 8). Bu nedenle, 8’in 2 tabanlı logaritması 3’tür (log2⁸ = 3). Logaritmalar genellikle 10’luk tabanla yazılmaktadır.

• log1= 0
• log10= 1
• log100= 2
• log1000= 3 gibi.

Yukarıdaki logaritmik sonuçları incelediğimizde sonuçların birbirinde kat kat fazla olduğunu görüyoruz. Log1 ile log3 karşılaştırıldığında, 3’ün 1’in 100 katı olduğu görülmektedir. Bunun yanında daha başka logaritma özellikleri de bulunmaktadır. Aşağıda bu özellikleri incelemeniz için hazırladığımız yazı, sizlere yardımcı olacaktır.

Logaritma Fonksiyonunun Tanımı Nedir?

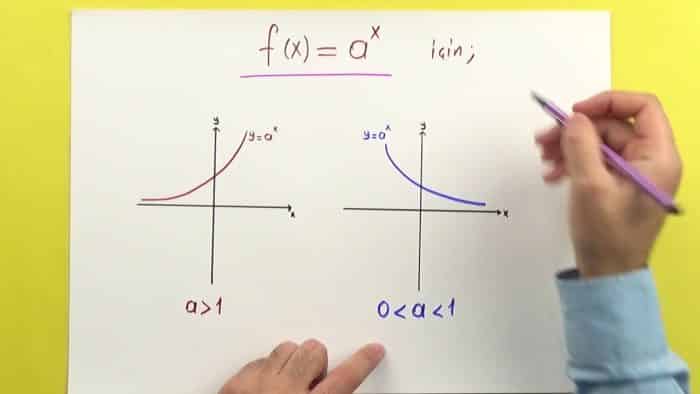
Logaritma fonksiyonun tanımlı olduğu noktalar bulunmaktadır. Logaritma fonksiyonu R⁺ dan R’ye tanımlı bir fonksiyondur. Yani bu ifadeden anlaşıldığı gibi sadece pozitif sayıların logaritması bulunmaktadır. Logaritma fonksiyonu ve üstel fonksiyon birbirinin tersi fonksiyonlardır. Üstel fonksiyonun bütün özellikleri logaritma özellikleri olarak da karşınıza çıkmaktadır.

Ayrıca sitemizden matematik testini çözebilirsiniz.

Logaritma Fonksiyonunun Tanımlı Özellikleri Nelerdir?

Logaritma özellikleri belirli noktalarda tanımlılık göstermektedir. Aşağıda bu özelliklere ulaşabilirsiniz:

• Her a eleman R⁺ – {1} olmak üzere, 1’den farklı her a pozitif reel sayının a tabanına göre logaritması 1 olarak bulunur.
  1. log_aa= 1.
• Taban fark etmeksizin, 1’şn logatması her zaman 0’dır.
  1. log_a1= 0.
• Her a elaman R⁺ – {1} ve her b elaman R⁺ ve x,y elaman R olmak üzere;
  1. log_aⁿb^m = m/n log_ab’dir.
• Pozitif reel sayıların çarpımının logaritmasına bakarsak, bu sayıların logaritmaları toplamını buluruz.
  1. log_a(x.y)= log_ax+ log_by’dir.
• Pozitif reel sayıların bölümünün logaritmasına bakarsak, bu sayıların logaritmaları farklarını buluruz.
  1. log_a(x/y)= log_ax- log_by’dir.
• a, m elaman R⁺ – {1}, b elaman R⁺ ise,
  1. log_ab= log_cb/log_ca’dır.
• log_ab=1/log_b
• log_a log_ba= log_ac.
• Her a eleman R⁺ – {1} olmak üzere,
  1. a ^logab=b

10)Her a elaman R⁺ – {1}, a ve c eleman R⁺ olmak üzere,

1. a) a^log_b^c= c^log_b^a’dır.

Logaritma İle İlgili Video Anlatımı

Logaritma Fonksiyonunun Tanım Kümesi Nedir?

Logaritma fonksiyonunun tanımlı olduğu değerler kümesi aşağıdaki gibidir:

• Her a eleman R⁺ – {1} olmak üzere,

f: R -> R⁺, f(x)= a^x biçiminde tanımlanıyor olan üstel fonksiyonun tersi alındığında logaritmik fonksiyonu buluruz.

f^-1: R⁺ -> R, f^-1(x)= log_ax şeklinde gösterilmektedir.

Yani, logaritma fonksiyonunun tabanı sıfırdan ve 1’den farklı bir sayı olması gerekmektedir.

y= log_ax Fonksiyonunun Şartları Nelerdir?

• a> 0,
• a sayısı 1’ eşit olamaz.
• x> 0.

Yukarıdaki şartların hepsi sağlandığı zaman logaritma fonksiyonunu yazabilirsiniz.

Neler Logaritmik Fonksiyon Olarak Tanımlanmaktadır?

Logaritmik fonksiyon olarak sayılan bazı değerler şunlardır:

• Richer ölçeği,
• Asit ve bazlık ölçümü (pH),
• Ses yoğunluk ölçümü (Desibel, dB).

Matematik soru çözme programı detaylarına da bakabilirsiniz.

Günlük Yaşantımızda Logaritmanın Yeri Var Mıdır?

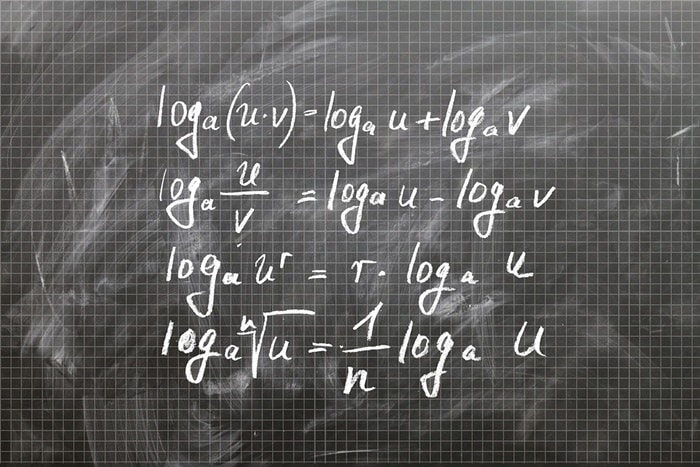
Gerçek hayatta logaritmalar, genellikle çok büyük veya çok küçük sayıları anlamak için kullanılır. Örneğin, güneşin parlaklığı metrekare başına 100.000 lümendir. Geceleri görülebilen en parlak yıldızın parlaklığı metrekare başına 0,00005 lümendir. Çok büyük veya çok küçük sayılar, karşılaştırmayı anlamamızı logaritma sağlayacaktır. Bu örnek için sayısal logaritma sonucunu içeren bir ölçek geliştirirsek, güneşin parlaklığı 5 (log10100.000) ve gece görülen en parlak Sirius’un parlaklığı -4.3 (log100.00005) olur. Bu şekilde, sayıların anlaşılması kolaylaşır. Logaritma özellikleri ile bu karşılaştırmaların daha fazla çeşidi, daha kolay bir şekilde bulunmaktadır.

Logaritma Özellikleri Sıkça Sorulan Sorular: